Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
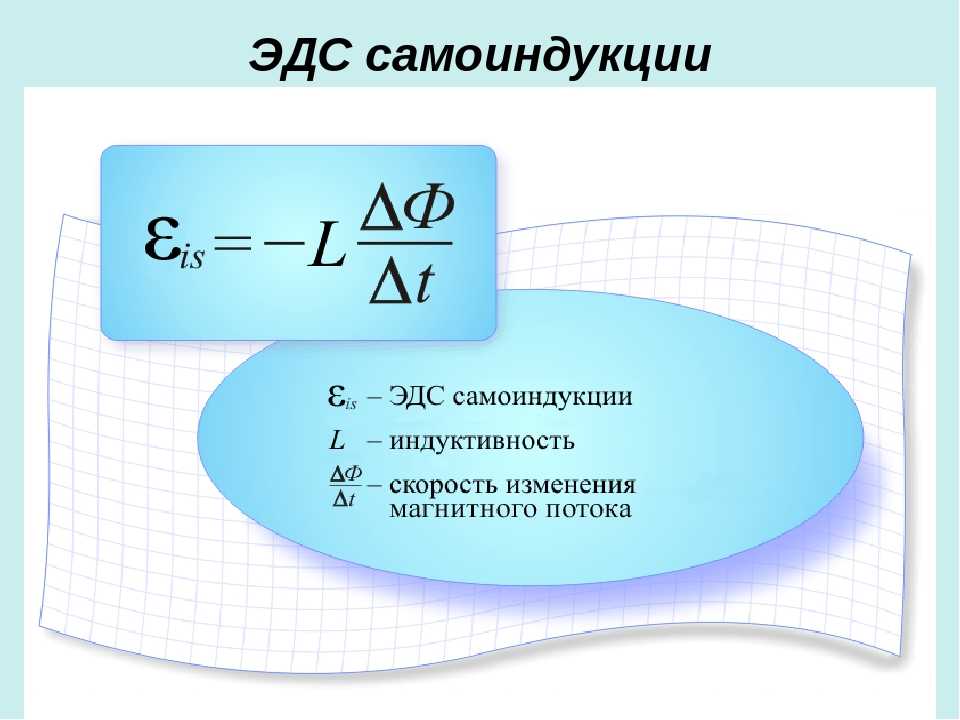
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно! Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
Ce = C : (1 — 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
![]()
Появление понятия магнитной индукции
На заре эпохи развития электричества люди стали исследовать сопутствующие явления. Так, Ханс Эрстед в 1819 году обнаружил: проводник с током создает вокруг круговое магнитное поле, Андре-Мари Ампер показал, что если направление движения зарядов совпадает, соседствующие проводники притягивают друг друга. Конец спорам положило создание закона Био-Савара (отечественные источники добавляют Лапласа), описывающего величину, направление магнитной индукции в точке пространства. Источники допускают оговорку касательно того, что исследования велись постоянного тока.
![]()
Взаимосвязь индукции и напряженности магнитного поля
Интегрирование (см. рисунок) идет по контуру с током. В формуле r подразумевает элементарную среднюю точку текущего отрезка, r0 – место пространства, для которого вычисляется магнитная индукция
Обратите внимание, в знаменателе дроби за интегралом перемножаются два вектора. Результатом выходит величина, направление которой определим по правилу буравчика (левой или правой руки)
Интегрирование ведется по элементу контура dr, r – средняя точка малого отреза полной длины. Идентичные разности в числителе и знаменателе сократим, остается вверху единичный вектор, задающий направление результата.
Формула показывает, как найти поле для контуров любой формы, проводя интегрирование по точкам. Современные численные методы лежат в основе действия компьютерных приложений (наподобие Maxwell 3D) по решению соответствующей задачи. Уравнение согласуется с законами Гаусса (магнитной индукции) и Ампера (циркуляции магнитного поля). Георг Ом использовал знания о компасе, выводя известную зависимость. Форму линий поля получим при помощи магнитных стрелок и силы оставления направления неизменным (см. заметку про закон Ома для участка цепи). Это будет картина магнитной индукции в пространстве, экспериментально подтвердившая закон Био-Савара-Лапласа.
Позволило сделанное Амперу в 1825 году показать: электрический ток в некоторых случаях является аналогом постоянного магнита. Появилась новая модель, которая лучше согласовывалась с действительностью, нежели схема диполей Пуассона. Подобная абстракция объясняла отсутствие в природе изолированных магнитных полюсов. По современным представлениям, кусок стали намагничивается, оттого что диполи элементарных частиц и молекул приобретают упорядоченность. На этом основаны контуры размагничивания сердечников трансформаторов, которые перед выключением питания вызывают затухающие колебания тока. В результате эффект упорядоченности размывается, выраженные свойства пропадают.
![]()
Спин электрона
Наличие магнитного момента объясняется существованием спинов (понятие введено в 20-х годах XX века) – угловой момент частиц микромира. Реальные, не абстрактные вещи, существование подтверждено экспериментально (Штерн-Герлах). Спин является векторной величиной, одинаковой для всех частиц одного типа (например, электронов), описывается специальным квантовым числом. В СИ единицей измерений служит Дж с, как и для другого углового момента (постоянной Планка). Иногда применяется упрощенная безразмерная запись. Постоянная Планка опускается. Указывается просто спиновое квантовое число (s, ms).
Благодаря наличию спина, элементарная частица обзаводится магнитным моментом, вычисляемым по формуле: в числителе произведение спинового углового момента на заряд частицы и g-фактор (постоянные, приводимые в различных справочниках для тех или иных элементарных частиц); в знаменателе – удвоенная масса элементарной частицы. Как видите, поддается учету, максимальную намагниченность материала в заданных условиях можно заранее рассчитать. Настоящим триумфом квантовой электродинамики явилось предсказание g-факторов для некоторых элементарных частиц.
Открытие Майклом Фарадеем в 1831 году генерации переменным магнитным полем кругового электрического показало: два явления тесно связаны, что явилось предпосылкой созданию (четырех) уравнений Максвелла, частным случаем которых являются большинство формул в этой области, считая упомянутые выше. Исследования шли своим чередом, но несколько разными путями. Интеграцию произвел лорд Кельвин, известный как Вильям Томпсон, который показал наличие H (напряженность) и B магнитной индукции, первая характеризует модель Пуассона, вторая – Ампера.
https://youtube.com/watch?v=2oKBbt8W7PM
Физический смысл магнитной индукции
Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.
Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится)
Влияние числа витков и способа намотки
Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:
- большим количеством витков на единицу длины;
- укрупнением поперечного сечения;
- установкой в центральной части сердечника с ферромагнитными характеристиками.
От чего зависит индуктивность катушки, примеры типовых решений
Индуктивность одновиткового контура и индуктивность катушки
Для расчета элементарной конструкции подойдет преобразованная первая формула:
Ф = L * I.
Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:
Ψ = n * Ф.
Аналогичным образом:
Ln = L1 * n.
В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.
Индуктивность соленоида
Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.
Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:
- количества витков (N);
- тока (i);
- плотности намотки (n – число контуров на единицу длины);
- площади поперечного сечения (S);
- объема (V = S * l).
Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):
- В = m0 * N * (i/l) = m0 * n * I;
- Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
- L = m0 * N2 * (S/l) = m0 * n2 * V.
Индуктивность тороидальной катушки (катушки с кольцевым сердечником)
Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:
L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),
где:
- 2π * rL – длина рабочего элемента со средним радиусом rL;
- R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.
Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.
СДЕЛАЕМ УПРОЩЕННЫЙ РАСЧЕТ ТРАНСФОРМАТОРА 220/36 ВОЛЬТ.
Мощность во вторичной цепи: Р_2 = U_2 · I_2 = 60
ватт
Где:Р_2
– мощность на выходе трансформатора, нами задана 60 ватт
;
U
_2
— напряжение на выходе трансформатора, нами задано 36 вольт
;
I
_2
— ток во вторичной цепи, в нагрузке.
КПД трансформатора мощностью до 100 ватт
обычно равно не более η = 0,8
.КПД определяет, какая часть мощности потребляемой от сети идет в нагрузку. Оставшаяся часть идет на нагрев проводов и сердечника. Эта мощность безвозвратно теряется.
Определим мощность потребляемую трансформатором от сети с учетом потерь:
Р_1 = Р_2 / η = 60 / 0,8 = 75 ватт
.
Мощность передается из первичной обмотки во вторичную через магнитный поток в магнитопроводе.Поэтому от значения
Р_1
, мощности потребляемой от сети 220
вольт,
зависит площадь поперечного сечения магнитопровода S
.
Магнитопровод – это сердечник Ш – образной или О – образной формы, набранный из листов трансформаторной стали. На сердечнике будут располагаться первичная и вторичная обмотки провода.
Площадь поперечного сечения магнитопровода рассчитывается по формуле:
S = 1,2 · √P_1.
Где:S
— площадь в квадратных сантиметрах,
P
_1 — мощность первичной сети в ваттах.
S = 1,2 · √75 = 1,2 · 8,66 = 10,4 см².
По значению S
определяется число витков w
на один вольт по формуле:
w = 50/S
В нашем случае площадь сечения сердечника равна S = 10,4 см.кв.
w = 50/10,4 = 4,8
витка на 1 вольт.
Рассчитаем число витков в первичной и вторичной обмотках.
Число витков в первичной обмотке на 220 вольт:
W1 = U_1 · w = 220 · 4.8 = 1056 витка.
Число витков во вторичной обмотке на 36 вольт:
W2 = U_2 · w = 36 · 4,8 = 172.8 витков
,
округляем до 173 витка
.
В режиме нагрузки может быть заметная потеря части напряжения на активном сопротивлении провода вторичной обмотки. Поэтому для них рекомендуется число витков брать на 5-10 % больше рассчитанного. Возьмем W2 = 180 витков.
Величина тока в первичной обмотке трансформатора:
I_1 = P_1/U_1 = 75/220 = 0,34 ампера
.
Ток во вторичной обмотке трансформатора:
I_2 = P_2/U_2 = 60/36 = 1,67 ампера.
Диаметры проводов первичной и вторичной обмоток определяются по значениям токов в них исходя из допустимой плотности тока, количества ампер на 1 квадратный миллиметр площади проводника. Для трансформаторов плотность тока,
для медного провода,
принимается 2 А/мм² .
При такой плотности тока диаметр провода без изоляции в миллиметрах определяется по формуле: d = 0,8√I
.
Для первичной обмотки диаметр провода будет:
d_1 = 0,8 · √1_1 = 0,8 · √0,34 = 0,8 · 0,58 = 0,46 мм. Возьмем 0,5 мм
.
Диаметр провода для вторичной обмотки:
d_2 = 0,8 · √1_2 = 0,8 · √1,67 = 0,8 · 1,3 = 1,04 мм. Возьмем 1,1 мм.
ЕСЛИ НЕТ ПРОВОДА НУЖНОГО ДИАМЕТРА,
то можно взять несколько, соединенных параллельно, более тонких проводов. Их суммарная площадь сечения должна быть не менее той, которая соответствует рассчитанному одному проводу.
Площадь поперечного сечения провода определяется по формуле:
s = 0,8 · d².
где
: d — диаметр провода
.
Например: мы не смогли найти провод для вторичной обмотки диаметром 1,1
мм.
Площадь поперечного сечения провода диаметром 1,1
мм. равна:
s = 0,8 · d² = 0,8 · 1,1² = 0,8 · 1,21 = 0,97 мм²
.
Округлим до 1,0
мм².
Из
таблицы
выбираем диаметры двух проводов сумма площадей сечения которых равна 1.0 мм².
Например, это два провода диаметром по 0,8 мм
. и площадью по0,5 мм²
.
Или два провода: — первый диаметром 1,0 мм
. и площадью сечения 0,79 мм²
,
— второй диаметром 0,5 мм
. и площадью сечения 0,196 мм²
.что в сумме дает: 0,79 + 0,196 = 0,986 мм².
Намотка катушки ведется двумя проводами одновременно, строго выдерживается равное количество витков обоих проводов. Начала этих проводов соединяются между собой. Концы этих проводов также соединяются.
Получается как бы один провод с суммарным поперечным сечением двух проводов.
Смотрите статьи:
— «Как намотать трансформатор на Ш-образном сердечнике».
— «Как изготовить каркас для Ш — образного сердечника».
Электрический аппарат — трансформатор используется для преобразования поступающего переменного напряжения в другое — исходящее, к примеру: 220 В в 12 В (конкретно это преобразование достигается использованием понижающего трансформатора). Прежде чем разбираться с тем, как рассчитать трансформатор, вы в первую очередь должны обладать знаниями о его структуре.
Простейший трансформатор является компоновкой магнитопровода и обмоток 2-х видов: первичной и вторичной, специально намотанных на него. Первичная обмотка воспринимает подающееся переменное напряжение от сети (н-р: 220 В), а вторичная обмотка, посредством индуктивной связи создает другое переменное напряжение. Разность витков в обмотках влияет на выходное напряжение.